Table of Contents
ToggleIntroduction
Pharmacalculations are the backbone of accurate and safe pharmacy practice. From calculating drug dosages to preparing IV fluids and understanding pharmacokinetics, Pharmacalculations ensure precision in every step of pharmaceutical care. For pharmacy students, mastering Pharmacalculations is not just an academic requirement—it is a life-saving skill that directly impacts patient safety and treatment outcomes.
This complete guide explores 12 powerful topics in Pharmacalculations that every pharma student must learn to build confidence, accuracy, and efficiency in their professional journey.

1. Basic Foundations of Pharmacalculations
Every student begins with the basics. Pharmacalculations start with understanding:
Units of measurement (Metric, Apothecary, Avoirdupois systems)
Conversion of weight, volume, and length
Ratio and proportion method
Dimensional analysis
✅ Example: Convert 2.5 g to mg → 2.5 × 1000 = 2500 mg.
Mastering these fundamentals of Pharmacalculations creates a strong base for more advanced calculations.
2. Dosage Calculations
Correct drug dosage is a critical aspect of Pharmacalculations. Topics include:
Pediatric dose calculations (Young’s Rule, Clark’s Rule, BSA method)
Adult dose adjustments (weight-based, BSA-based)
Loading dose and maintenance dose
Adjustments for renal and hepatic impairment
✅ Example: Clark’s Rule → Child dose = (Weight in lbs ÷ 150) × Adult dose.
Pharmacalculations in dosage ensure patients receive safe and effective therapy.
Read more: Pharmacalculations
3. Concentration and Dilution Calculations
Another core part of Pharmacalculations is concentration preparation. Students learn:
Dilution formulas (C1V1 = C2V2)
Stock and working solutions
Reconstitution of powders
Expressing concentrations (% solutions, molarity, normality, ppm, ppb)
✅ Example: To prepare 500 mL of 5% solution from a 25% stock → V1 = (5 × 500) ÷ 25 = 100 mL.
These Pharmacalculations are used daily in compounding and hospital practice.
4. Parenteral and IV Fluid Calculations
Pharmacalculations extend to IV therapy, where precision is vital. Students practice:
Flow rate (mL/hr, drops/min)
Infusion times and volumes
Osmolarity and isotonicity
Electrolyte calculations (Na⁺, K⁺, Ca²⁺)
✅ Example: 1000 mL IV fluid over 8 hours → 1000 ÷ 8 = 125 mL/hr.
Without accurate Pharmacalculations, IV errors can cause serious harm.
5. Compounding and Formulation Calculations
In pharmacy labs, Pharmacalculations help prepare mixtures, creams, emulsions, and suppositories. Key concepts include:
Alligation method (alternate & medial)
Geometric dilution
Displacement value for suppositories
✅ Example: To prepare 70% alcohol (1000 mL) from 95% and 30%, use the alligation method.
Pharmacalculations in compounding bridge the gap between theory and practical pharmacy.
6. Pharmacokinetics Calculations
Pharmacokinetics is the science of drug movement in the body. Students must learn:
Volume of distribution (Vd)
Clearance (Cl)
Half-life (t½)
Steady-state concentration
Area under the curve (AUC)
✅ Example: Half-life = (0.693 × Vd) ÷ Cl.
Pharmacalculations in pharmacokinetics help design safe dosing regimens.
7. Industrial and Manufacturing Pharmacalculations
Pharma production also relies on accurate Pharmacalculations:
Batch size and yield
Drying time (tray, vacuum, FBD)
Tablet compression (hardness, friability, weight variation)
Capsule fill weight and capacity
Sterilization and F0 value
✅ Example: Yield = (Actual ÷ Theoretical) × 100.
Pharmacalculations in industry maintain quality and consistency in drug manufacturing.
8. Biopharmaceutical Calculations
Biopharmaceutics focuses on how drugs interact in the body. Pharmacalculations here include:
Therapeutic index (TI)
Protein binding percentage
Partition coefficient
MEC & MTC levels
✅ Example: TI = TD50 ÷ ED50.
These Pharmacalculations show the safety margin of medicines.
9. Radiopharmaceutical Calculations
Radioactive drugs demand special Pharmacalculations:
Half-life of isotopes
Radioactive decay law
Radiation dose measurements
✅ Example: A drug with a 6-hour half-life → only 25% remains after 12 hours.
Accuracy in Pharmacalculations is essential for nuclear medicine.
10. Clinical Pharmacy Calculations
In hospitals, clinical Pharmacalculations are used daily:
Creatinine clearance (Cockcroft–Gault formula)
BMI calculations
Corrected calcium
Acid-base balance
Parenteral nutrition
✅ Example: Creatinine Clearance = ((140 − age) × weight) ÷ (72 × SCr).
Pharmacalculations in clinical settings prevent dosing errors and support patient safety.
11. Miscellaneous Pharmacalculations
Other important areas include:
Specific gravity and density
Molecular weight & equivalent weight
Isotonicity adjustments
Powder flow properties (Carr’s Index, Hausner ratio)
✅ Example: Specific Gravity = Weight of substance ÷ Weight of equal volume of water.
Even small details matter in Pharmacalculations.
👉 This list covers academic, clinical, and industrial aspects of pharmaceutical calculations.
Complete Explanation of Pharmaceutical Calculations
1. Basic Foundations
Units of Measurement
Pharmacy relies heavily on accurate measurements.
Metric System: Most widely used (grams, liters, meters, etc.).
Apothecary System: Older system (grains, drams, ounces).
Avoirdupois System: Common for weight in commerce (pounds, ounces).
👉 Example:
1 pound (avoirdupois) = 16 ounces = 454 grams
Conversion of Units
You must often convert between systems.
1 mg = 0.001 g
1 L = 1000 mL
1 grain ≈ 65 mg
Ratio and Proportion Method
Used when scaling up or down a dose.
👉 Formula:
A/B=C/D
Percentage Calculations
w/w (weight/weight): g of solute in 100 g of product
w/v (weight/volume): g of solute in 100 mL of solution
v/v (volume/volume): mL of solute in 100 mL of solution
👉 Example: 5% w/v NaCl = 5 g NaCl in 100 mL solution
2. Dosage Calculations
Pediatric Dose Calculations
Children require smaller, weight-based doses.
Adult Dose Adjustments
Based on body weight (mg/kg) or body surface area (mg/m²).
Loading Dose & Maintenance Dose
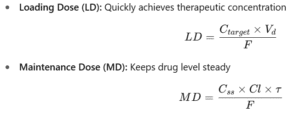
3. Concentration Calculations
Dilution (C1V1 = C2V2)
Used when preparing solutions.
👉 Example: How much of 10% NaCl is needed to make 100 mL of 5%?
10×V1=5×100 ⟹ V1=50mL
Stock Solution Preparation
Start with a concentrated solution → dilute to desired strength.
Reconstitution
Powdered drugs must be mixed with solvent.
👉 Example: Add 10 mL sterile water to vial to get 250 mg/mL concentration.
Expressing Concentrations
Molarity (M): moles/L
Molality (m): moles/kg solvent
Normality (N): equivalents/L
ppm (parts per million): mg/L
4. Parenteral & IV Fluid Calculations
Flow Rate
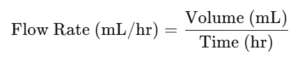
Drop Rate
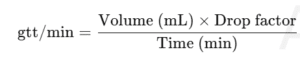
Osmolarity
![]()
Isotonicity
Important for injections and eye drops.
Methods: NaCl equivalent method, cryoscopic method.
5. Compounding & Formulation Calculations
Alligation Method
Used to prepare a mixture of different concentrations.
Alligation Medial: To find average strength.
Alligation Alternate: To mix two solutions to get desired strength.
Displacement Value
For suppositories.
DV=Weight of drug/Weight of base displaced
Powder Blending
Uses geometric dilution for uniform mixing.
6. Pharmacokinetics Calculations
Volume of Distribution (Vd)

Clearance (Cl)

Half-Life (t½)
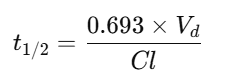
AUC (Area Under Curve)
Represents total drug exposure.
Steady-State Concentration (Css)
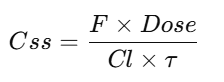
7. Industrial & Manufacturing Calculations
Batch Size & Yield

Drying Time
Depends on moisture content, drying constant, and equipment used.
Tablet Compression
Weight variation, hardness, friability, disintegration time.
Capsule Filling
Depends on bulk density, shell size, and fill weight.
Sterilization (F0 Value)
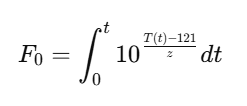
8. Biopharmaceutical Calculations
Therapeutic Index:
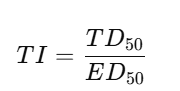
Protein Binding: % bound = (Bound drug / Total drug) × 100
Partition Coefficient: Ratio of drug solubility in oil vs water.
9. Radiopharmaceutical Calculations
Radioactive Decay:
![]()
Half-Life (t½):
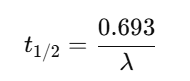
10. Clinical Pharmacy Calculations
BMI:
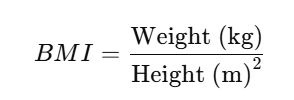
Creatinine Clearance (Cockcroft-Gault):
![]()
Corrected Calcium:
![]()
Parenteral Nutrition: Calculation of amino acids, dextrose, lipids, electrolytes.
11. Miscellaneous Calculations
Density & Specific Gravity:
SG = Weight of substance / Weight of equal volume of waterMolecular & Equivalent Weight:
Equivalent weight = Molecular weight / n (valence factor)Isotonicity:
NaCl equivalent method to adjust solutions.Powder Flow (Carr’s index, Hausner ratio):
Measures compressibility and flow property.
✅ That’s a complete explanation of all pharmaceutical calculations, from basic to advanced (clinical + industrial).

1) Basic Foundations
Example 1 — Unit conversions
Convert 2.5 g to mg; 750 mL to L; 3 grains to mg.
1 g = 1000 mg → 2.5 g = 2500 mg
1 mL = 0.001 L → 750 mL = 0.75 L
1 grain ≈ 65 mg → 3 grains ≈ 195 mg
Example 2 — Percent strength (w/v)
How many grams of NaCl are needed to prepare 250 mL of 8% w/v?
8% w/v = 8 g per 100 mL →
grams=8×250/100=20g
Example 3 — Ratio strength to percent
Convert 1:500 to % w/v.
%=1/500×100=0.2%
2) Dosage Calculations
Example 1 — Clark’s rule (weight-based)
Adult dose = 500 mg; child weighs 66 lb.
Child dose=66/150×500=220 mg
Example 2 — Young’s rule (age-based)
Adult dose = 240 mg; child is 6 years.
Child dose=6/(6+12)×240=80 mg
Example 3 — BSA method
Adult dose = 100 mg; child BSA = 0.80 m².
Child dose=0.80/1.73×100≈46.24 mg
3) Concentrations, Dilution & Preparation
Example 1 — C1V1=C2V2
Make 500 mL of 5% from a 25% stock.
V1=C2*V2/C1=5×500/25=100 mL
→ Take 100 mL of 25% + 400 mL diluent.
Example 2 — Molar solution
Prepare 250 mL of 0.5 M NaCl (MW 58.44).
grams=M×L×MW=0.5×0.25×58.44=7.305 g
Example 3 — Normal solution
How many grams of H₂SO₄ to make 1 L of 1 N?
Valence = 2 → Eq wt = 98.079/2 = 49.04
grams=N×L×Eq wt=1×1×49.04≈49.04 g
4) Parenteral & IV Fluids
Example 1 — Infusion rate (mL/hr)
1000 mL over 8 hours.
1000/8=125 mL/hr
Example 2 — Drop rate (gtt/min)
500 mL over 4 hours; drop factor 20 gtt/mL.
gtt/min=500×20/240≈41.7 gtt/min
Example 3 — Osmolarity
D5W (5% dextrose): 5 g/100 mL → 50 g/L; dextrose does not dissociate.
Osmolarity=50/180.156×1000≈277.5 mOsm/L
5) Compounding & Formulation
Example 1 — Alligation (make 70% alcohol, 1000 mL from 95% & 30%)
Parts: 95−70=2595-70=2595−70=25, 70−30=4070-30=4070−30=40 → ratio low:high = 25:40 = 5:8
95% volume = 8/13×1000=615.38 mL
30% volume = 5/13×1000=384.62 mL
Example 2 — Suppository displacement value
Mold capacity 2.0 g; drug 300 mg/supp; DV (drug) = 1.5; 12 supps.
Base displaced per supp = 0.300/1.5=0.200 g
Base per supp = 2.0−0.200=1.800g
For 12: Base 21.6 g; Drug 3.6 g
Example 3 — Ointment from stock
30 g of 2% w/w using 10% stock.
Stock=0.02×30/0.10=6 g; Base=24 g
6) Pharmacokinetics
Example 1 — Loading dose (LD)
Target Ctarget=15 mg/L; Vd=40L; F=0.5.
LD=15×40/0.5=1200 mg
Example 2 — Half-life
Vd=70L; Cl=5 L/hr.
t1/2=0.693*70/5 ≈ 9.70 hr
Example 3 — Average steady-state concentration (intermittent dosing)
Dose 500 mg q8h IV; Cl=6 L/hr.
Cˉss=F×Dose/(Cl×τ)=1×500/(6×8)≈10.42 mg/L
7) Industrial & Manufacturing
Example 1 — Percent yield
Theoretical 10.0 kg; actual 8.6 kg.
%Yield=8.6/10.0×100=86%
Example 2 — Vacuum drying (falling-rate model)
Approximate first-order moisture removal on a dry-basis:
M0=30%, M=5%, Me=2%, k=0.35 h−1
![]()
Example 3 — Tablet press output
45-station rotary press at 30 rpm.
Tablets/min = 45×30=1350
In 2 hours → 1350×120=162,000
8) Biopharmaceutics
Example 1 — Therapeutic index
TD50=200mg; ED50=50mg.
TI=200/50=4
Example 2 — Protein binding
Total = 20 mg/L; free = 3 mg/L.
Bound% =(20−3)/20×100=85%
Example 3 — Partition coefficient (shake-flask)
Octanol: 200 mg/100 mL; Water: 20 mg/100 mL.
P=(200/100)/(20/100)=10
9) Radiopharmaceuticals
Example 1 — Activity after time
![]()
Example 2 — Time to reach 25% of initial
![]()
Example 3 — Required initial to have 5 mCi after 8 h
![]()
10) Clinical Pharmacy
Example 1 — Creatinine clearance (Cockcroft–Gault)
Male, 65 y, 80 kg, SCr = 1.2 mg/dL.
CrCl=(140−65)×80/(72×1.2)≈69.4 mL/min
Example 2 — Corrected calcium
Measured Ca = 8.2 mg/dL; Albumin = 2.5 g/dL.
Cacorr=8.2+0.8(4−2.5)=9.4mg/dL
Example 3 — Parenteral nutrition dextrose calories
2,000 mL of D20W.
D20W = 20 g/100 mL → grams = 0.20×2000=400 g
Calories =400×3.4=1360 kcal
11) Miscellaneous
Example 1 — Specific gravity
50 mL liquid weighs 60 g.
SG=60/50=1.20
Example 2 — ppm
0.02% w/v expressed as ppm.
0.02% = 0.02 g/100 mL = 0.2 g/L = 200 mg/L = 200 ppm
Example 3 — Isotonicity (NaCl equivalent method)
30 mL of 1% drug solution; E=0.18E=0.18E=0.18. How much NaCl to add?
NaCl needed for isotonicity: 0.009×30=0.2700.009\times 30=0.2700.009×30=0.270 g
NaCl “provided” by drug: 0.300×0.18=0.0540.300\times 0.18=0.0540.300×0.18=0.054 g
Add: 0.270−0.054=0.216 g NaCl
Here’s a comprehensive FAQ section covering all major categories of pharmaceutical calculations. Each answer is simple, precise, and practical—so it can serve as a quick reference or learning guide.
Conclusion
Pharmacalculations are the foundation of accuracy, safety, and efficiency in the pharmacy profession. From calculating pediatric doses to preparing IV fluids, compounding formulations, and understanding pharmacokinetics, every step in pharmaceutical practice relies on precise Pharmacalculations.
For pharmacy students, mastering these 12 powerful topics in Pharmacalculations is not just an academic exercise but a professional necessity. Strong calculation skills reduce errors, improve patient safety, and build confidence in both clinical and industrial settings.
By practicing regularly and applying Pharmacalculations in real-world scenarios, students and professionals can ensure they are fully prepared to handle the challenges of modern pharmacy with accuracy and confidence.
Frequently Asked Questions (FAQs) on Pharmaceutical Calculations
Basic Foundations
Q1: Why do pharmacists use different systems of measurement?
Because medicines are used globally, pharmacists encounter the metric, apothecary, and avoirdupois systems. Conversions ensure accuracy when different units appear on prescriptions.
Q2: What is the difference between % w/w, % w/v, and % v/v?
% w/w: grams of solute per 100 g of solution.
% w/v: grams of solute per 100 mL of solution.
% v/v: mL of solute per 100 mL of solution.
Q3: How do I convert ratio strength to percentage?
%=1/denominator×100
Example: 1:500 → 0.2%
Dosage Calculations
Q4: Which method is best for calculating pediatric doses?
The BSA method is considered most accurate because it accounts for body surface area, not just age or weight.
Q5: What is the difference between a loading dose and a maintenance dose?
Loading dose: Quickly achieves therapeutic level.
Maintenance dose: Keeps the level steady over time.
Q6: Why is body weight often used for dose adjustments?
Because drug metabolism and distribution depend on patient’s weight and body composition.
Concentration & Dilution
Q7: How do I calculate the volume needed from a stock solution?
Use C1V1 = C2V2, where C = concentration and V = volume.
Q8: What is the difference between molarity and molality?
Molarity (M): Moles per liter of solution.
Molality (m): Moles per kilogram of solvent.
Q9: Why is isotonicity important?
Isotonic solutions prevent cell damage, pain, and irritation in injections and eye drops.
Parenteral & IV Fluids
Q10: How is IV flow rate calculated?
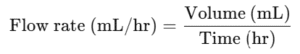
Q11: What are “gtt/min” in IV therapy?
It refers to drops per minute delivered, based on the set’s drop factor.
Q12: What does osmolarity measure?
It measures the concentration of solute particles in a solution (mOsm/L).
Compounding & Formulation
Q13: What is the alligation method used for?
To prepare a solution of desired strength by mixing two or more solutions of different strengths.
Q14: What is displacement value in suppository calculations?
It shows how much base a drug displaces. Example: If 0.3 g drug displaces 0.2 g base, DV = 1.5.
Q15: Why is geometric dilution important in compounding powders?
It ensures uniform distribution of small quantities of potent drugs.
Pharmacokinetics
Q16: What is volume of distribution (Vd)?
It’s a theoretical volume indicating how widely a drug distributes in body tissues compared to plasma.
Q17: What is clearance (Cl)?
The rate at which a drug is removed from the plasma.
Q18: Why is half-life important?
It determines dosing intervals and how long a drug remains active in the body.
Industrial & Manufacturing
Q19: What is yield in manufacturing?
The percentage of actual output vs theoretical output.
Q20: Why are drying time calculations important?
They prevent over-drying or under-drying of materials, which affects stability and quality.
Q21: What is F0 in sterilization?
It’s the lethality value representing equivalent sterilization at 121°C.
Biopharmaceutical Calculations
Q22: What is therapeutic index (TI)?

It shows the safety margin of a drug.
Q23: What is protein binding, and why does it matter?
Protein-bound drugs are inactive; only free drug exerts therapeutic effect.
Q24: What is a partition coefficient?
It measures drug lipophilicity—important for absorption across cell membranes.
Radiopharmaceuticals
Q25: How is radioactivity measured?
In curies (Ci) or becquerels (Bq).
Q26: How do you calculate remaining activity after time?
Use the formula:
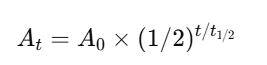
Q27: Why is half-life critical in radiopharmaceuticals?
It is due to radioactive decay determines dosage accuracy and safety.
Clinical Pharmacy
Q28: What is the Cockcroft-Gault formula used for?
To estimate creatinine clearance and adjust drug dosing in kidney impairment.
Q29: Why do we calculate corrected calcium?
Because low albumin can make total calcium appear falsely low.
Q30: What is included in parenteral nutrition calculations?
Carbohydrates (dextrose), proteins (amino acids), fats (lipids), electrolytes, vitamins, and minerals.
Miscellaneous
Q31: What is specific gravity (SG)?
It is the density of a substance compared to water.
Q32: How do you calculate ppm?
1 ppm = 1 mg/L in water solutions.
Q33: Why is Carr’s index used?
It measures powder compressibility and flow properties for tableting.
